SPS Knowledge Bank

a collection of resources written by your professors to help you succeed in your classes

Category: Math

Calculator Usage/Etiquette  

By Chandra Mongroo, Ph.D, Full-time Faculty and Doctoral Lecturer, General Education

This page provides guidance on the appropriate use of calculators, highlighting circumstances where reliance on estimation or algebraic rearrangement may be more advantageous prior to resorting to calculator assistance. By emphasizing the importance of conceptual understanding and procedural fluency, we suggest that calculators should be more of an auxiliary tool rather than primary instrument in problem-solving.

Identifying the appropriate moments to utilize a calculator is crucial for efficiently arriving at solutions in mathematics. While many topics necessitate calculator usage, instances may arise where the problem isn’t immediately conducive to direct input into the calculator. This scenario often occurs when using formulae that require solving for a variable in terms of the others beforehand. Consequently, having a solid grasp of algebraic manipulation is important. Below is a classic example that illustrates this concept, emphasizing the importance of proficiency in algebraic techniques before relying on calculator assistance. 

Example: Consider the following annuity formula from a finance module. 

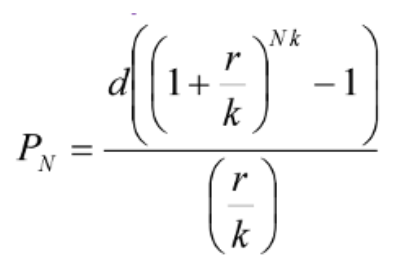
Suppose we have values for all variables and need to solve for d. The following equation reflects substitution of all known numerical values. 

800000 = [d((1 + 0.06/12)^30(12) - 1)]/(0.06/12)

Here is an extra resource on solving a variable in terms of the others: https://youtu.be/fnuIT7EhAvs 

We are tasked with solving for d. It is recommended to isolate for d. Breaking this down step by step: 

a. Multiply both sides of the equation by (0.06/12):

800000(0.06/12) = d((1 + 0.06/12)30(12) – 1)

b. Divide both sides by the expression being multiplied by d. 

d = 800000(0.06/12) / ((1 + 0.06/12)30(12) - 1)

At this moment, we may use a scientific or graphing calculator to simplify this further. 

Using a calculator you will have two routes: 

  1. With proper parentheses placement, input all the values as such: [800000*(.06/12)]/[((1+.06/12)^30(12))-1]. It may look very cumbersome, and it is! This method is not advised at first. 
  1. Breaking down the expression step by step working first on simplifying the numerator, then on the denominator abiding by the order of operations. 

numerator = 4,000

denominator = 5.02257521226 ≈ 5.0226

*Note: There will be some rounding error in the calculation. This results from the calculator’s inability to represent the entire string of digits of the number if it is irrational. The less decimal places used in the rounded expression, the more final error that will appear in the solution. 

*Tip: A decent number of decimal places to carry throughout is 4 decimal places (or to the ten thousandths place). 

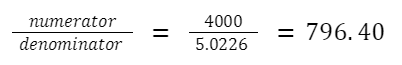
numerator / denominator = 4000 / 5.0226 = 796.40

Resource on rounding errors: https://users.wpi.edu/~goulet/MME523/roundoff.htm

Introduction to writing in mathematics 

By Chandra Mongroo, Ph.D, Full-time Faculty and Doctoral Lecturer, General Education

Writing in mathematics is an essential skill that serves to communicate abstract concepts, proofs, and problem-solving methodologies effectively. Unlike writing in literature, mathematical writing demands precision, clarity, and logical coherence to convey mathematical ideas accurately. This distinct approach to writing underscores the importance of articulating mathematical reasoning and procedures concisely, ensuring that mathematical arguments are both comprehensible and rigorous

Writing an essay in a math class? Not sure where to begin? Here is a helpful resource for engaging in mathematical writing: A Guide to Writing Mathematics (UC Davis).

A General Outline for a Mathematical Essay

  • Introduction: Restate the problem in your own words. Be sure to include vocabulary that is important to the problem.
    • Background Information: Provide context around the problem. Careful not to assume that the reader has full knowledge on the topic. Avoid words such as “obvious” since this assumes the knowledge of your reader. You may include relevant details that will help the reader understand the problem you are presenting. In addition, this section is where specific vocabulary or notation/ symbols are defined. Establishing the definitions, it is safe to use throughout the body of the paper.  
    • Thesis Statement: Restate the goal of the problem in one sentence. This serves as a quick reminder to the reader what you will be attempting to answer. 
  • Body: In this section, you will elaborate your approach and perspective of the problem.
    • Supporting Paragraphs: A good approach to this section would be to break down the problem into various subproblems. The more details that you provide, the more clarity the reader has into your perspective. You should be as elaborate as possible! 
  • Conclusion: This section provides the culminating idea of your paper.
    • Summarize/Review key points: In this section you want to cycle back to the original objective of the problem, that is return to the thesis statement. Provide a small synopsis of your perspective of the problem, and provide emphasis of the conclusion. Make sure that your reader understands how you arrived at your final solution. 
  • Concluding thoughts: You may want to conclude with other ideas that you considered while thinking about the problem. Alternatively, you may leave your reader with questions that you have after the analysis of the problem. This is a good place to provide your experiences of reasoning throughout the problem.

General problem solving 

By Chandra Mongroo, Ph.D, Full-time Faculty and Doctoral Lecturer, General Education

This page offers diverse problem-solving approaches in mathematics, recognizing that different methods suit different situations or learning preferences. Having a range of strategies fosters flexibility, enriches understanding, and cultivates resilience, preparing individuals to tackle complex problems effectively across various contexts.

A. Review of Problem Solving Process: Polya’s Problem Solving Techniques (Berkeley Math)

Q: I read the math question but do not know where to start. How do I proceed?

A: The key is to unlock the theme of the question. Here are some suggestions on how to begin: 

  1. Gather as much knowledge as possible from the problem. Highlight or underline key words. This is where you should return to the text and review the unit’s vocabulary.
  2. Re-visit worked out examples. Pay close attention to details in the problem solving process that are not clearly stated. Write out these steps with explanations in your notes. 
  3. Return to the question you were tasked with and approach it in a similar way as the text. 
  4. Analyze your solution. What did you solve? What does it mean in the context of the problem? Is it reasonable with the given constraints? 
  5. Report your results. Writing out a summary of your findings will help you reinforce the ideas that were developed in the problem solving process.

B. General Problem Solving Heuristics

A heuristic is a general strategy for solving a problem. Here you will find various examples of heuristics for problem solving (Ohio State University). 

Worked Examples (Lippman)

C. Estimating Solutions

When problem solving, it is suggested to have an idea of your solution when you attempt a problem. Estimating solutions isolates concept application from numerical accuracy. Below are some useful videos. 

  1. Estimating Whole Number Sum & Differences
  2. Estimating Decimal Addition
  3. Estimating Decimal Differences
  4. Estimating Whole Number Products
  5. Estimating Decimal Products

You may find the term “significant digits”, “significant figures”, or “sig figs” in a math or science related course. We say significant figures are specific digits in a number that are used to express precision.  

Useful resources:

  1. Practicing Sig Figs (Purdue University)
  2. A Short Guide to Sig Figs (Yale University)
  3. Worked Examples (Libre Texts)

Introduction to writing in mathematics

March 8, 2024 / / 0 Comments

Writing an essay in a math class? Not sure where to begin? Here is a helpful resource for engaging in mathematical writing: A Guide to Writing Mathematics (UC Davis).

A General Outline for a Mathematical Essay 

Introduction: Restate the problem in your own words. Be sure to include vocabulary that is important to the problem. 

Background Information: Provide context around the problem. Careful not to assume that the reader has full knowledge on the topic. Avoid words such as “obvious” since this assumes the knowledge of your reader. You may include relevant details that will help the reader understand the problem you are presenting. In addition, this section is where specific vocabulary or notation/ symbols are defined. Establishing the definitions, it is safe to use throughout the body of the paper.  

Thesis Statement: Restate the goal of the problem in one sentence. This serves as a quick reminder to the reader what you will be attempting to answer. 

Body: In this section, you will elaborate your approach and perspective of the problem. 

Supporting Paragraphs: A good approach to this section would be to break down the problem into various subproblems. The more details that you provide, the more clarity the reader has into your perspective. You should be as elaborate as possible! 

Conclusion: This section provides the culminating idea of your paper. 

Summarize/Review key points: In this section you want to cycle back to the original objective of the problem, that is return to the thesis statement. Provide a small synopsis of your perspective of the problem, and provide emphasis of the conclusion. Make sure that your reader understands how you arrived at your final solution. 

Concluding thoughts: You may want to conclude with other ideas that you considered while thinking about the problem. Alternatively, you may leave your reader with questions that you have after the analysis of the problem. This is a good place to provide your experiences of reasoning throughout the problem.
A general outline for a mathematical essay 

© 2025 SPS Knowledge Bank

Theme by Anders Noren — Up ↑