By Michael FitzGerald, Ph.D, Professor of Philosophy, General Education
The following handout explains a crucial skill in critical thinking.
Category: Academic Resources
By Chandra Mongroo, Ph.D, Full-time Faculty and Doctoral Lecturer, General Education
This page provides guidance on the appropriate use of calculators, highlighting circumstances where reliance on estimation or algebraic rearrangement may be more advantageous prior to resorting to calculator assistance. By emphasizing the importance of conceptual understanding and procedural fluency, we suggest that calculators should be more of an auxiliary tool rather than primary instrument in problem-solving.
Identifying the appropriate moments to utilize a calculator is crucial for efficiently arriving at solutions in mathematics. While many topics necessitate calculator usage, instances may arise where the problem isn’t immediately conducive to direct input into the calculator. This scenario often occurs when using formulae that require solving for a variable in terms of the others beforehand. Consequently, having a solid grasp of algebraic manipulation is important. Below is a classic example that illustrates this concept, emphasizing the importance of proficiency in algebraic techniques before relying on calculator assistance.
Example: Consider the following annuity formula from a finance module.
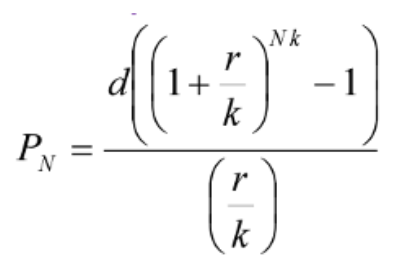
Suppose we have values for all variables and need to solve for d. The following equation reflects substitution of all known numerical values.
![800000 = [d((1 + 0.06/12)^30(12) - 1)]/(0.06/12)](https://openlab.sps.cuny.edu/knowledge-bank/wp-content/uploads/sites/110/2024/04/image-4.png)
Here is an extra resource on solving a variable in terms of the others: https://youtu.be/fnuIT7EhAvs
We are tasked with solving for d. It is recommended to isolate for d. Breaking this down step by step:
a. Multiply both sides of the equation by (0.06/12):
800000(0.06/12) = d((1 + 0.06/12)30(12) – 1)
b. Divide both sides by the expression being multiplied by d.
At this moment, we may use a scientific or graphing calculator to simplify this further.
Using a calculator you will have two routes:
- With proper parentheses placement, input all the values as such: [800000*(.06/12)]/[((1+.06/12)^30(12))-1]. It may look very cumbersome, and it is! This method is not advised at first.
- Breaking down the expression step by step working first on simplifying the numerator, then on the denominator abiding by the order of operations.
numerator = 4,000
denominator = 5.02257521226 ≈ 5.0226
*Note: There will be some rounding error in the calculation. This results from the calculator’s inability to represent the entire string of digits of the number if it is irrational. The less decimal places used in the rounded expression, the more final error that will appear in the solution.
*Tip: A decent number of decimal places to carry throughout is 4 decimal places (or to the ten thousandths place).
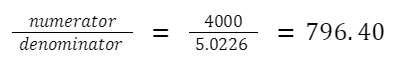
Resource on rounding errors: https://users.wpi.edu/~goulet/MME523/roundoff.htm
By Gabriela Smeureanu, Ph.D, Doctoral Lecturer, General Education Undergraduate Adviser, Chemistry Department, Hunter College
Math skills reader
This reader provides a clear overview of the foundational math skills necessary for success in General Chemistry.
How to write a lab report
10 awesome study skills
By Michael FitzGerald, Ph.D, Professor of Philosophy, General Education
Below are some resources specifically for Philosophy writing assignments. For more general resources applicable to any writing class, please see the following pages: Reference/citation managers, Finding reputable popular sources, and Resources on improving your writing.
Library databases specific to Philosophy:
- Resource: PhilPapers
- Description: PhilPapers is a comprehensive index and bibliography of philosophy maintained by professional philosophers. The collection includes journals, books, and open access archives. The index, the largest open access archive in philosophy, currently contains 2,826,241 entries categorized in 5,858 categories. PhilPapers also can be used to manage and generate citations for philosophical works.
Resources on improving your Philosophy writing:
- Resource: “Writing Philosophy: A Student’s Guide to Reading and Writing Philosophy Essays” by Lewis Vaughn.
- Description: This book is a primer on composition in philosophy, with helpful practical tips and examples for undergraduate students, as well as guidance on how to read and critique argumentative essays. It also includes:
- A rulebook that describes the basic principles of good writing;
- A reference guide to common writing errors and skills;
- Advice on avoiding biased and discriminatory language;
- A chapter on commonly confused words; and
- Sections entitled “How to Argue Online” and “When Partisanship Wrecks You.”
- Resource: “Writing Philosophy Papers: A Student Guide”
- Description: This handbook is a free student guide to writing philosophy papers, created by the Department of Philosophy at Oregon State University. It provides guidance on how to write a variety of different forms of philosophical prose. For example, when asked to write a philosophical précis, students can use this booklet to structure their summary. Proper citation form for philosophical references is also discussed.
- Resource: Peter Horban (Simon Fraser University) — “Writing a Philosophy Paper” (i.e., a brief paper)
- Description: Horban’s guide offers specific advice on structuring paragraphs in philosophical writing.
- Resource: D.W. Portmore (Professor of Philosophy at Arizona State University) – “Tips on Writing A Philosophy Paper”
- Description: Portmore focuses on (1) the ability to comprehend, reconstruct, and analyze complex philosophical arguments; (2) the ability to critically evaluate such arguments; (3) the ability to argue persuasively for one’s own views; and (4) the ability to articulate one’s own thoughts in a clear, concise, and well-organized manner.
Finding reputable popular sources in Philosophy:
- Resource: The Philosophers’ Magazine
- Description: The Philosophers’ Magazine (TPM) is an independent quarterly, devoted to presenting academic philosophy in an accessible, non- technical format. It includes interviews with leading philosophers, as well as news, essays, reviews, and regular columnists. Notable for its depth, clarity, and accessibility, TPM distributed in the U.S. and Canada by the highly-reputable Philosophy Documentation Center.
By Chandra Mongroo, Ph.D, Full-time Faculty and Doctoral Lecturer, General Education
Writing in mathematics is an essential skill that serves to communicate abstract concepts, proofs, and problem-solving methodologies effectively. Unlike writing in literature, mathematical writing demands precision, clarity, and logical coherence to convey mathematical ideas accurately. This distinct approach to writing underscores the importance of articulating mathematical reasoning and procedures concisely, ensuring that mathematical arguments are both comprehensible and rigorous
Writing an essay in a math class? Not sure where to begin? Here is a helpful resource for engaging in mathematical writing: A Guide to Writing Mathematics (UC Davis).
A General Outline for a Mathematical Essay
- Introduction: Restate the problem in your own words. Be sure to include vocabulary that is important to the problem.
- Background Information: Provide context around the problem. Careful not to assume that the reader has full knowledge on the topic. Avoid words such as “obvious” since this assumes the knowledge of your reader. You may include relevant details that will help the reader understand the problem you are presenting. In addition, this section is where specific vocabulary or notation/ symbols are defined. Establishing the definitions, it is safe to use throughout the body of the paper.
- Thesis Statement: Restate the goal of the problem in one sentence. This serves as a quick reminder to the reader what you will be attempting to answer.
- Body: In this section, you will elaborate your approach and perspective of the problem.
- Supporting Paragraphs: A good approach to this section would be to break down the problem into various subproblems. The more details that you provide, the more clarity the reader has into your perspective. You should be as elaborate as possible!
- Conclusion: This section provides the culminating idea of your paper.
- Summarize/Review key points: In this section you want to cycle back to the original objective of the problem, that is return to the thesis statement. Provide a small synopsis of your perspective of the problem, and provide emphasis of the conclusion. Make sure that your reader understands how you arrived at your final solution.
- Concluding thoughts: You may want to conclude with other ideas that you considered while thinking about the problem. Alternatively, you may leave your reader with questions that you have after the analysis of the problem. This is a good place to provide your experiences of reasoning throughout the problem.
By Chandra Mongroo, Ph.D, Full-time Faculty and Doctoral Lecturer, General Education
This page offers diverse problem-solving approaches in mathematics, recognizing that different methods suit different situations or learning preferences. Having a range of strategies fosters flexibility, enriches understanding, and cultivates resilience, preparing individuals to tackle complex problems effectively across various contexts.
A. Review of Problem Solving Process: Polya’s Problem Solving Techniques (Berkeley Math)
Q: I read the math question but do not know where to start. How do I proceed?
A: The key is to unlock the theme of the question. Here are some suggestions on how to begin:
- Gather as much knowledge as possible from the problem. Highlight or underline key words. This is where you should return to the text and review the unit’s vocabulary.
- Re-visit worked out examples. Pay close attention to details in the problem solving process that are not clearly stated. Write out these steps with explanations in your notes.
- Return to the question you were tasked with and approach it in a similar way as the text.
- Analyze your solution. What did you solve? What does it mean in the context of the problem? Is it reasonable with the given constraints?
- Report your results. Writing out a summary of your findings will help you reinforce the ideas that were developed in the problem solving process.
B. General Problem Solving Heuristics
A heuristic is a general strategy for solving a problem. Here you will find various examples of heuristics for problem solving (Ohio State University).
Worked Examples (Lippman)
C. Estimating Solutions
When problem solving, it is suggested to have an idea of your solution when you attempt a problem. Estimating solutions isolates concept application from numerical accuracy. Below are some useful videos.
- Estimating Whole Number Sum & Differences
- Estimating Decimal Addition
- Estimating Decimal Differences
- Estimating Whole Number Products
- Estimating Decimal Products
You may find the term “significant digits”, “significant figures”, or “sig figs” in a math or science related course. We say significant figures are specific digits in a number that are used to express precision.
Useful resources:
- Practicing Sig Figs (Purdue University)
- A Short Guide to Sig Figs (Yale University)
- Worked Examples (Libre Texts)
Writing an essay in a math class? Not sure where to begin? Here is a helpful resource for engaging in mathematical writing: A Guide to Writing Mathematics (UC Davis).
| A General Outline for a Mathematical Essay Introduction: Restate the problem in your own words. Be sure to include vocabulary that is important to the problem. Background Information: Provide context around the problem. Careful not to assume that the reader has full knowledge on the topic. Avoid words such as “obvious” since this assumes the knowledge of your reader. You may include relevant details that will help the reader understand the problem you are presenting. In addition, this section is where specific vocabulary or notation/ symbols are defined. Establishing the definitions, it is safe to use throughout the body of the paper. Thesis Statement: Restate the goal of the problem in one sentence. This serves as a quick reminder to the reader what you will be attempting to answer. Body: In this section, you will elaborate your approach and perspective of the problem. Supporting Paragraphs: A good approach to this section would be to break down the problem into various subproblems. The more details that you provide, the more clarity the reader has into your perspective. You should be as elaborate as possible! Conclusion: This section provides the culminating idea of your paper. Summarize/Review key points: In this section you want to cycle back to the original objective of the problem, that is return to the thesis statement. Provide a small synopsis of your perspective of the problem, and provide emphasis of the conclusion. Make sure that your reader understands how you arrived at your final solution. Concluding thoughts: You may want to conclude with other ideas that you considered while thinking about the problem. Alternatively, you may leave your reader with questions that you have after the analysis of the problem. This is a good place to provide your experiences of reasoning throughout the problem. |
